尋找新奇的量子物态，如拓撲絕緣體、反常量子霍爾效應、外爾半金屬等，是近年來凝聚态物理和材料科學領域的研究熱點。例如，拓撲絕緣體具有受拓撲保護的零能隙邊界态，在無能耗傳輸、新型量子器件等方向上有廣泛的應用前景。一般地，對于d維n階的拓撲絕緣體而言，會在其（d-n）維的邊界上出現邊界态。但由于制造工藝等條件的限制，這些拓撲材料在實際應用方面面臨嚴峻挑戰。針對這一難題，利用集總參數電子線路中基爾霍夫方程與凝聚态物理緊束縛哈密頓量的對應關系，可以在傳統的電子線路中設計出種類豐富的新型拓撲物态。此外，電路具有器件功能多樣，制備工藝成熟、可靠等諸多優勢，可以實現和驗證傳統凝聚态體系中難以實現或無法實現的物态（如非厄密拓撲态、高維拓撲态），為探索新奇量子物态及其實際應用提供了一個理想的平台。

近期，beat365英国官网网站beat365英国官网网站本科生姚俊傑在周苗教授的指導下，在拓撲電路的理論設計方面取得重要進展。通過理論計算，設計出一種類似凝聚态物理中凱庫勒晶格的電路結構（圖1），使電路的動力學特征矩陣具有與其哈密頓量一緻的形式。有趣的是，可以通過調控電容值來實現拓撲相變，在電路意義下的能帶裡出現非零的四極矩，實現二維二階拓撲絕緣體。相關研究成果以“Quadrupole topological phase and robust corner resonance in Kekulé hexagonal electric circuit”為題發表在專業物理領域的國際知名期刊New Journal of Physics上（論文鍊接：https://iopscience.iop.org/article/10.1088/1367-2630/abae88）。

圖1設計的凱庫勒六角電路結構

工作系統研究了一維半無限長電路和零維具有開放邊界條件的有限大電路，在二者中分别發現了能隙非常小的邊緣态和無能隙角落态，且該角落态的拓撲起源是非零的體四極矩，而不是由邊緣偶極極化引起的瓦尼爾類角落态。同時，通過對體系電壓分布的計算，發現電路的拓撲态能夠通過外加輸入的激勵頻率來靈活調控。當電路處于共振頻率時，體系的兩點電阻會在角落處出現一個極大的共振峰，為實驗觀察提供了一個極大的利好（圖2）。在電路的實際應用時，不可避免地會出現器件參數的誤差，該工作發現此電路對于一定程度内的誤差具有良好的魯棒性，拓撲态在該範圍内不受影響，且電路的尺寸也可以做到很小而不導緻拓撲态消失。這些發現對于未來拓撲電路實際研究和應用有重要的指導意義。

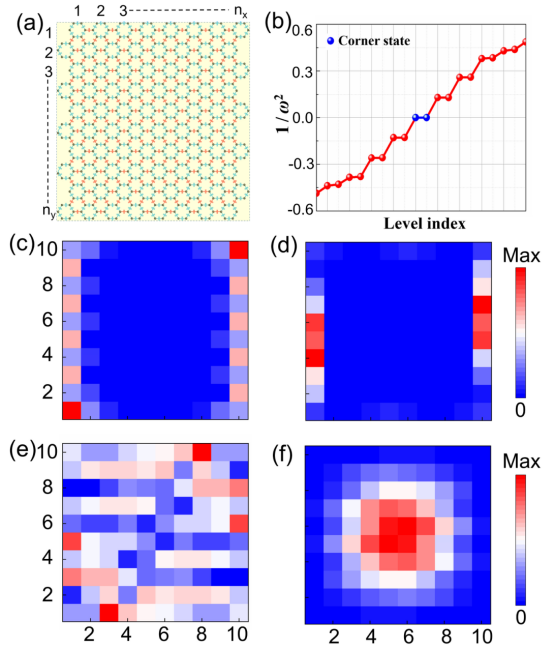
圖2: (a) 0維電路示意圖; (b)對應的能級分布; (c)-(f)不同激勵頻率下的電壓分布

該論文的第一作者姚俊傑是beat365英国官网网站beat365英国官网网站2017級本科生。姚俊傑同學學習成績優異，排名物理專業大班第1，獲得包括國家勵志獎學金（2018）、暑期社會實踐校級二等獎及先進個人（2018）、北京市數學競賽二等獎（2018），國家獎學金（2019），校級優秀生和學習優秀特等獎（2019），馮如杯科技競賽二等獎（2020）等多個獎項及榮譽。姚俊傑積極參與科研活動，主要從事通過傳統電路實現高維高階拓撲态、自旋軌道耦合效應、冷原子系統等方向的理論研究。